Rl, david silver lec2,3 헷갈리는거 정리, optimal value function

**motivation: ** lecture 2,3. bellman optimality equation이랑 DP의 control iteration에 대해서 알아보자.

강의영상: https://www.youtube.com/watch?v=PnHCvfgC_ZA

최적 policy를 어떻게 찾는가.

모든 policy에 대해서, a = max_x(f(x)) 라는 뜻은, for all x, f(x)의 최대값을 a에 저장한다.

즉 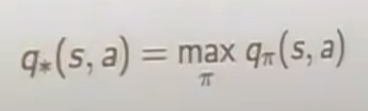해당 s, a일 때, 가장 높은 reward는 무엇인가.

결국, q star를 알면, 끝난다. MDP

결국에는 q star를 알면, 어느 곳으로 갈지를 안다. 왜? reward가 80인 곳을 가지, 70인 곳을 가지는 않을 것이니깐.

식1,2, optimal svf, avf

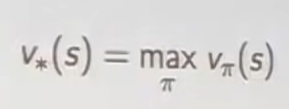
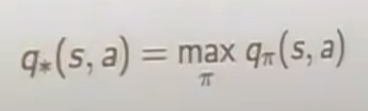
식3, optimal policy

식4,5,6,7 bellman optimality equation for v_, q_ func

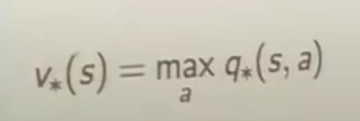
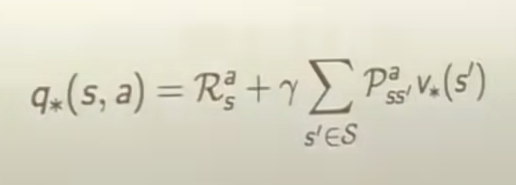
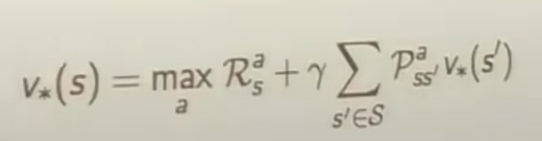
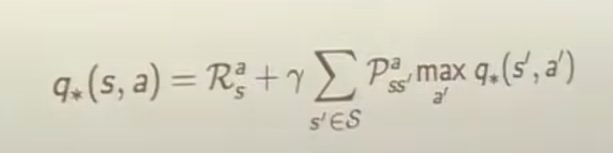
BEE는 평균으로 구할 수 있었는데, BOE를 푸는 것은 불가능하다. 왜? non-linear equation이기 때문에. max와 expectation이 섞여있기 때문에, 그래서 no-closed form. 그래서 iterative solution methods. 가 있다.

value iteration 이해 안되서 추가

그냥 전통적인 알고리즘이라면 왼쪾 위에서부터 오른쪾 아래까지 사선으로 숫자를 매겨주면 될텐데, goal, loop, reward 떄문에, 모든 state에 대해서, 평가를 한다.

결국에는 value iteration은 모든 state(여기서는 15개의 state)에서 평가를 한다. 1번에서는, 우선 다 0으로 시작하고, 1번에서, 내가 어떤 state를 가던, 다 -1이다. 그래서 다 -1을 넣어준다.

v1—>2 상황에서는, 우선 

123

4567

891011

12131415 라고 할 때,

1번부터 보면, 자기가 옆으로 가니깐, -1이 되네? 즉 이 식에 의해서, 가장 max를 시키는 action을 수행하는 action에 대해서, 그냥 그 action value를 값을 가지게 된다.

optimal action value는 이렇게 되니깐. 그냥 다 더하는 것.

그래서, 그냥 -1로 고정되는 한편, 

2번 state에서는, 어디를 가던 다 -2가 된다. 그래서 -2로 update가 된다.

state-value function으로 bellman optimality eq를 쓰는 이유는 복잡도 때문인듯.

state-action pair: mn next-state-action pair mn 그래서 (mn)^2

DP를 설계할 수 있는 방법.

밑에있는 식의 오른ㄴ쪽 v(s’) 은 new value를 그냥 바로 넣는거다. 이렇게 하면 새로운 정보가 더 많아서, 더 효율적이게 된다. 그러면 어떻게 효율적으로 compute하기 위해서 ordering을 할까? 어떤 문제에 대해서는, 굉장히 더욱 효율적이게 되는 것이다.

new value function이 root,

old value function이 leaves

new value function이 root, old value function이 leaves

그래서 prioritize sweeping이라는 아이디어가 나온다.

이 아이디어는, mdp의 어떤 state의 update가 얼마나 중요한지에 대한 평가측도를 만드는 것이다.

그래서 어떤 것을 먼저 update해야 하는가? 그래서 priority queue를 줘서, 뭐가 더 중요한지 넣고, 그래서 그거 먼저 update하자다.

뭐가 더 중요한지를, bellman equation을 통해서 구한다.

직관은, 더 많이 state가 변하는 것은, 즉 0에서 1000까지 마지막에는 변하면, 그걸로 ordering을 한다.

real time dynamic programming

select the state that agent actually visit.

모든 것을 sweep하지 않고, agent를 실제 세계에 놓는다.

실제 tragactory를 random sample해서, 그 real sample 주변에서 update한다.

DP는 full-width backup을 사용한다.

모든 action과 모든 state를 본다. 이거는 굉장히 비쌈.

그리고 모든 tragectory를 보는 것이 아니라, sampliing을 할 것이다.

그래서 1 state도 compute하기가 어렵다. 백만개의 state가 있으면.

state - action - one sample로 backup할 것이다.

curse of dimensionality를 해결한다. sampling을 통해서.

그리고, 환경의 dynamic을 sampling 하니깐, 환경의 모델을 몰라도 된다.