ewc 코드 분석

motivation: ewc 코드를 분석해보자.

elastic weight consolidation.

fisher information이란 무엇인가. 이거를 알아야 할 필요가 있어 보여서, 분석을 해보겠다.

두개만 이해하면 된다. 1. EWC class, 2. ewc_train

EWC class

ewc_train

def ewc_train(model: nn.Module, optimizer: torch.optim, data_loader: torch.utils.data.DataLoader,
              ewc: EWC, importance: float):
    model.train()
    epoch_loss = 0
    for input, target in data_loader:
        input, target = variable(input), variable(target)
        optimizer.zero_grad()
        output = model(input)
        loss = F.cross_entropy(output, target) + importance * ewc.penalty(model)
        epoch_loss += loss.data[0]
        loss.backward()
        optimizer.step()
    return epoch_loss / len(data_loader)

importance * ewc.penalty(model) 이 부분만 추가로 loss에 추가가 되었다.

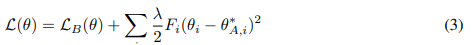
이거는 ewc 논문에 나온 수식. 여기서 두번째 항이 ewc.penalty(model)인 것 같다.

mle, maximum likelihood estimation

normal_train

def normal_train(model: nn.Module, optimizer: torch.optim, data_loader: torch.utils.data.DataLoader):
    model.train()
    epoch_loss = 0
    for input, target in data_loader:
        input, target = variable(input), variable(target)
        optimizer.zero_grad()
        output = model(input)
        loss = F.cross_entropy(output, target)
        epoch_loss += loss.data[0]
        loss.backward()
        optimizer.step()
    return epoch_loss / len(data_loader)

test

def test(model: nn.Module, data_loader: torch.utils.data.DataLoader):
    model.eval()
    correct = 0
    for input, target in data_loader:
        input, target = variable(input), variable(target)
        output = model(input)
        correct += (F.softmax(output, dim=1).max(dim=1)[1] == target).data.sum()
    return correct / len(data_loader.dataset)

EWC class

def variable(t: torch.Tensor, use_cuda=True, **kwargs):
    if torch.cuda.is_available() and use_cuda:
        t = t.cuda()
    return Variable(t, **kwargs)


class EWC(object):
    def __init__(self, model: nn.Module, dataset: list):

        self.model = model
        self.dataset = dataset

        self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
        self._means = {}
        self._precision_matrices = self._diag_fisher()

        for n, p in deepcopy(self.params).items():
            self._means[n] = variable(p.data)

    def _diag_fisher(self):
        precision_matrices = {}
        for n, p in deepcopy(self.params).items():
            p.data.zero_()
            precision_matrices[n] = variable(p.data)

        self.model.eval()
        for input in self.dataset:
            self.model.zero_grad()
            input = variable(input)
            output = self.model(input).view(1, -1)
            label = output.max(1)[1].view(-1)
            loss = F.nll_loss(F.log_softmax(output, dim=1), label)
            loss.backward()

            for n, p in self.model.named_parameters():
                precision_matrices[n].data += p.grad.data ** 2 / len(self.dataset)

        precision_matrices = {n: p for n, p in precision_matrices.items()}
        return precision_matrices

    def penalty(self, model: nn.Module):
        loss = 0
        for n, p in model.named_parameters():
            _loss = self._precision_matrices[n] * (p - self._means[n]) ** 2
            loss += _loss.sum()
        return loss

통계학에서(loss function이 아니라 likelihood를 썼을 때.) fisher information 정의

https://en.wikipedia.org/wiki/Informant_(statistics)

우선 fisher information은 score function의 variance를 의미한다. 우선 score function은 통계학에서, 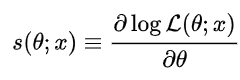이거를 의미하는데, 이거의 경우 theta가 1xm 차원의 row vector라면, 이거를 미분하게 되면, score function의 결과도 1xm 차원의 row vector가 된다. 즉 각 parameter 차원에 대해서 편미분하게 되는 것이다.

이 score function의 의미는, 해당 likelihood function에 대해서, theta의 값이 얼만큼의 영향을 주는지에 대한 값이다. score 값이 크면, theta의 값이 조금만 변해도, likelihood가 변한다는 것이다.

score function의 mean

근데 여기서 신기한 property가 나오는데, 모든 datapoint x에 대해서 평균을 내면, 이거는 0이 된다.

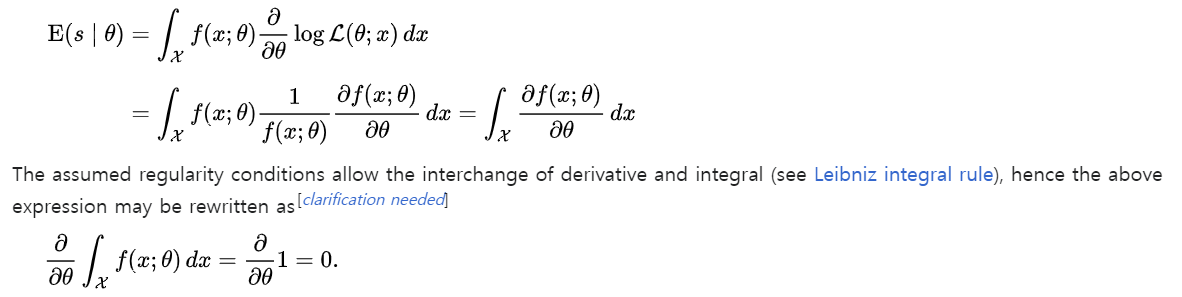
왜 mean이 0이 되냐하면, likelihood function을 그냥 적분하는 것이 되기 떄문에, likelihood function (스칼라) 에 대해서 theta로 편미분을 하게 되면, 1xm row vector로 나오고,

이거는 사실상 1 을 모든 parameter theta에 대해서 미분하게 되면, 1,m 벡터의 row vector가 나오게 된다.

FIM 첫번째 정의: score function의 variance

근데 중요한 것은, score function의 분산으로 FIM이 정의가 되는데, 이때 variance는 E[X^2] - E[X]^2 의 형태로 정의가 되는데, mean이 0이기 때문에, FIM은 사실상 E[X^2]으로 표현을 할 수 있다는 것이다.

FIM 두번째 정의: score function의 제곱의 평균

그래서 FIM의 두번째 정의는 –> I(theta)로 정의할 수 있다.

https://en.wikipedia.org/wiki/Fisher_information

이렇게 표현할 수 있다.

FIM 세번째 정의: score function의 두번 편미분의 평균의 음수.

근데 보면, 원래 fisher information의 평균은 0인 것을 알았다. 이것을 다시 theta에 대해서 편미분을 하면, 어처피 0인 것을 또 편미분 해도 0이다.

이 등식, 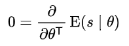이것을 계속 전개해 나가다 보면, 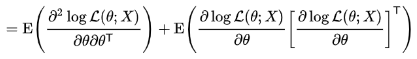이렇게 된다는 것. 이게 0임.

즉 fisher information의 원래 정의(오른쪽 term)은 사실 왼쪽 term의 minus를 붙인 것과 같다는 것이다.

ewc 논문 분석

내용/이미지 출처: EWC 논문(Kirkpatrick, James, et al. “Overcoming catastrophic forgetting in neural networks”, PNAS 2017.) 몇몇 이미지 출처: SOJEONG KIM blog, [Continual Learning] EWC

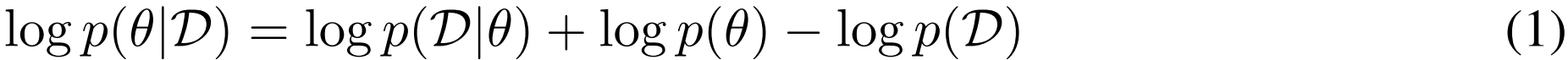
[!note] Note that the log probability of the data given the parameters log p(D|θ) is simply the negative of the loss function for the problem at hand −L(θ).

**이렇게, p(D

θ) 는 parameter가 주어졌을 때, data를 잘 설명하는 확률을 의미하는데, 근데 이거는 loss function, 즉 loss를 최소화하는 것과 같다고 하는 것.** –> 데이터 D에 대한 로그 우도가 최대화될 때 손실 함수 L(θ)가 최소화된다는 것을 의미. 즉, 모델이 데이터를 잘 설명할수록, 손실 함수의 값은 낮아짐.

이거는 특정 dataset이 주어졌을 때, parameter의 확률. 이렇게 볼 수 있는데, 이때, dataset이 $D_A$, $D_B$ 로 구성되어 있다고 하자.

그러면

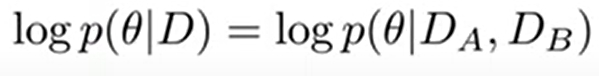
이렇게 표현 가능. 근데 여기서 dataset A와 B는 독립이라고 정의.

그러면, 독립이니깐, 이렇게 표현 가능.

그렇기 때문에,

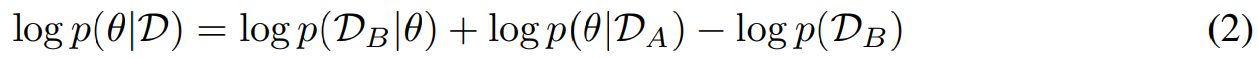
위 식 성립. 정리하자면

\[\log p(\theta|D) = \log p(\theta|D_A, D_B) = \log p(D_B | \theta) + \log p(\theta | D_A) - \log p(D_B)\]

first term

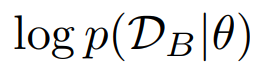이거는 task B 에 대한 loss다. (==L(θ) for dataset B.)

third term

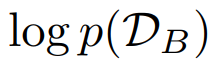이거는 dataset B에 대한 likelihood인데, 우리 optimization에서는 상수로 취급하는데, 왜냐하면 θ 와 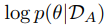에 의존(depend)하지 않기 때문이다.

second term

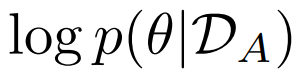이거는 task A에 대한 사후확률분포로, 어떤 parameter가 task A에 대해서 중요한지에 대한 값이다.

해석 출처: Alexey Kravets, EWC loss

그러면 이 각각의 term에 대한 해석은 완료했고. 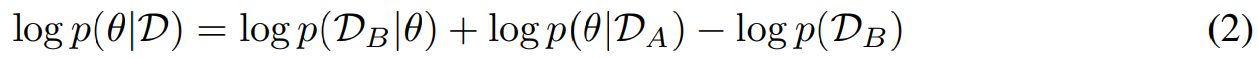third term은 무시 가능.

그러면 중요한 것은 가운데 term인 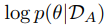이거를 어떻게 추정할 것이냐는 거다. 근데 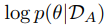이거는 intractable한데, 왜냐하면 모든 parameter space θ 에 대해서 적분을 해야하기 때문. 이거는 사실상 불가능.

그래서 normal 분포로 추정이 되고,

• 그 normal 분포의 mean은 task A에 대해 optimal한 성능을 가지는 theta($\theta_{A^*}$, paramter)의 평균으로,
• normal 분포의 variance는 Fisher information에서 가져온다.

이런 가정은 task A에서의 optimal한 분포와 task B에서의 optimal한 parameter가 별로 차이가 없을 것이라는 가정에서 시작됨.

 θꭺ* 에서, 몇몇의 parameter는 task A를 위해서 잘 작동하는, 굉장히 중요한 parameter들이 있을 것. 그래서 바뀌지 않기를 원함. FIM은, 특정 parameter가 ‘task A에 대한 loss’에 얼마나 영향을 끼치는지에 대한 값이다. 그래서 FIM이 큰 parameter의 변화가 큰 것에 대해서, taskB를 학습할 때에는 그 parameter를 학습하지 않도록 하는 것이다.

optimal weights for task A를 talyor expansion을 하면 이렇게 된다. 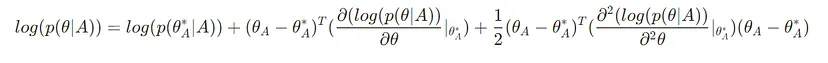우선 첫번쨰 term은, dataset A가 주어졌을 때, optimal parameter 의 확률이라서, 상수다. 바뀌지 않음.

두번쨰 term은, 계속 바뀌는 term이긴 한데, theta는 A에 대해서 optimal한 parameter이니깐, 편미분이 0이 된다. 0이라고 가정. 그래서 이 term도 없애면,

마지막 세번째 term만 살아남게 된다.

그러면 최종

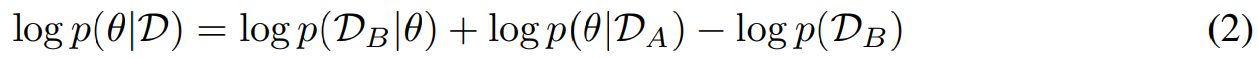
이 식은,

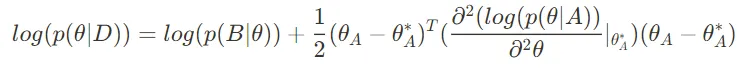
이렇게 변하게 된다.