bias variance tradeoff and belkin’s double descent curve

motivation: bias variance tradeoff and belkin’s double descent curve 를 이해하자.

1. bias variance tradeoff

bias variance tradeoff

이렇게, 실제 함수가 f(x)+error로 되어있다면,

mse의 경우에는, Error가 이렇게 나타나게 된다.

전개 과정을 설명하자면,

1. error는 다음과 같이 전개됨.

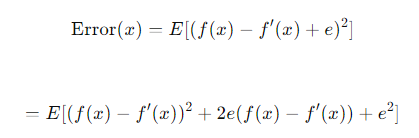
2. 제곱을 풀어 쓰면 이렇게 됨. 또한 가운데 항은 E[e]가 0이라고 가정하면 사라진다.

3. 그렇다면 왼쪽 식(E[(f(s) - f’(x))^2]은, 어떻게 bias^2 + variance가 되냐면,

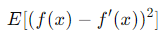이 식은 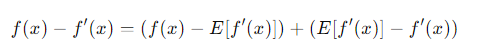이렇게 바꿀 수 있기 때문에,

제곱을 하게 되면, 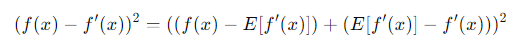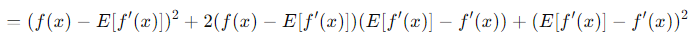이렇게 된다.

제곱을 해서, E를 씌우면 되는데,

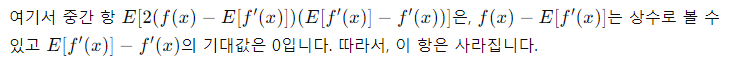
따라서 E를 씌우면,

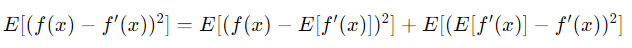
이런 식이 나온다. 우항의 왼쪽 식은 bias의 제곱, 오른쪽 항은 variance임을 볼 수 있다.

2. bias와 variance의 정의

정의를 자세하게 보면, Variance는 입력 데이터 x에 대한 variance가 아니라, f’(x)에 대한 variance다.

또한 Bias^2의 경우, 예측값과 정답값 간의 차이의 제곱인데, f(x)에는 E가 빠져있는 것을 볼 수 있다. 이거는 f(x)가 상수 취급을 당하기 때문이다.

질문: 그렇다면, 예측값에 대한 variance가 크다는 의미는, data에 대한 민감성이 크다는 의미인가?

지금 bias, variance tradeoff에서, model size가 x축으로 분석을 한다. 이때, dataset은 고정이라고 보는 것이 맞다.

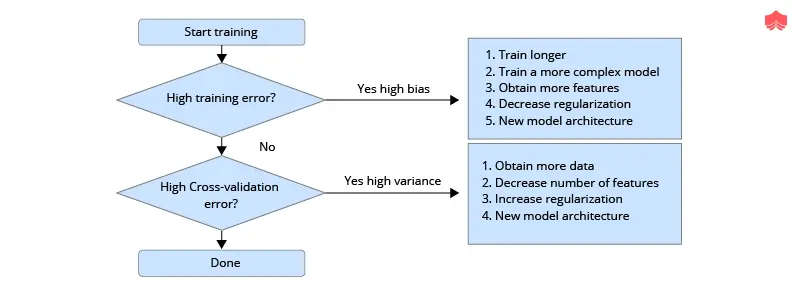
overfitting의 정의는, ML 모델이 훈련 데이터에 지나치게 적합되어서, 새로운 데이터나 테스트 데이터에는 성능이 저하되는 것을 의미한다. ovefitting의 특징에는, 1. train accuray가 굉장히 높고,(train loss가 작다.) 2. test accuracy가 굉장히 낮은 것이다.(test loss가 크다.) 3. 결국에는 data에 대한 민감도가 너무 크다는 것이다. 조금만 변화해도 출력값이 바뀐다. 민감도가 크다는 것은, 잡음(노이즈)도 학습한다는 것이다.

그래서, 노이즈도 학습해서, 민감도가 크게 되는데, 이렇게 되면, variance가 커지게 된다. 이것은 dataset이 고정되어야 성립하는 말이다.

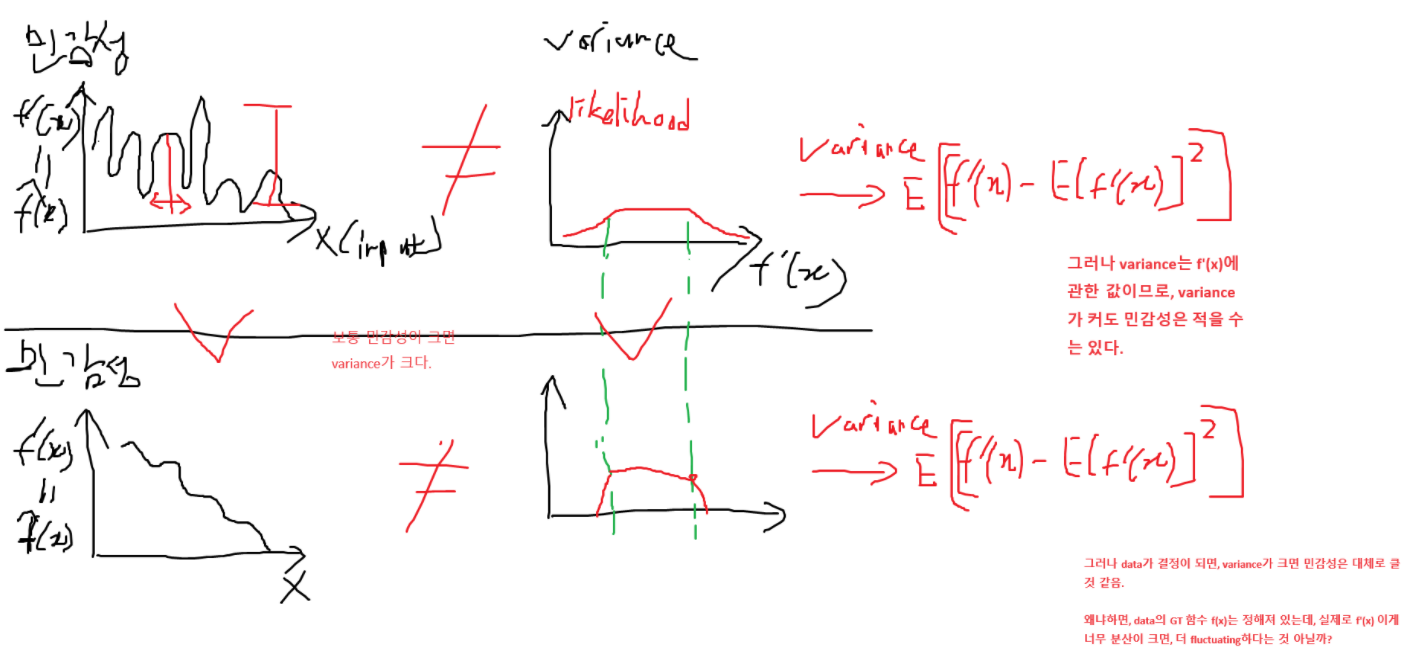
dataset이 고정되어 있으면, variance가 크면 보통은 민감도가 크다. (물론 overfitting regime에서의 말임. underfitting에서의 variance가 크다는 것은 학습이 안되었기 때문에 variance가 크다는 것.)

https://www.knowledgehut.com/blog/data-science/bias-variance-tradeoff-in-machine-learning

3. double descent curve

https://trivia-starage.tistory.com/239

DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT

early stopping은 validation loss가 더이상 줄어들지 않을 때, 끊는 것을 의미.

기존의 ML 연구자들은 더 큰 모델은 안좋은 성능을 낸다고 생각했었는데, 근데 실용적인 엔지니어들은, 모델은 크면 클수록 좋다는 생각을 하게 되었다. 그러나 중요한 것은, 특정 setting에서는 early stopping을 하면 test accuracy가 좋게 나오고, 어떤 setting에서는 zero training error까지 도달하도록 training을 시켜야 performance가 잘 나왔다는것이다. 그럼에도 불구하고, 전통적인 통계학자들과 DL practitioner들이 둘다 동의하는 것은, data가 더 많을수록 더 좋다는 것은 합의된 내용이다.

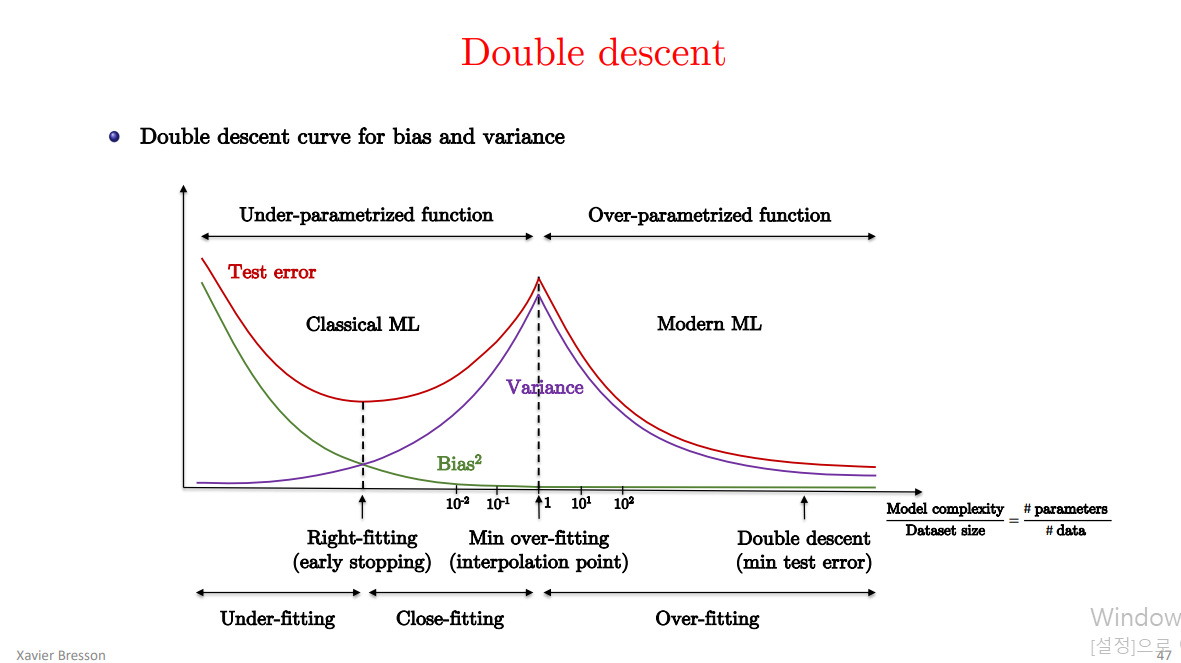
model complexity가 sample(입력 데이터)의 개수보다 작으면, (=under-parameterized regime) test error는 (x축이 model complexity, y축이 test error) U shape 모양을 띤다.(전통적인 bias/variance) tradeoff.

근데 model complexity가 sample의 개수보다 엄청 커지면, 그래서 training error를 0으로 만들 수 있따면, test error가 0으로 가게 된다. 그래서 더 큰 모델이 더 좋게 된다. 이것이 2018년 belkin이 처음 제시한 double descent curve다.

belkin’s double descent curve는 robust 현상이다. 다양한 task, architecture, optimization method 에 시도해 보았을 때, 비슷한 현상이 나온다. 또한 # of parameters 뿐만 아니라, Effective Model Complexity(EMC)를 정의한다.

훈련 과정의 EMC를, zero training error를 달성할 수 있는 maximum number of samples로 정의한다.

이 EMC는 data distribution과, classifier의 architecture에 종속적일 뿐만 아니라, 훈련 과정(training procedure)에도 영향을 받는다. (예를 들어서, training time을 늘리면 EMC도 증가한다.)

많은 natural model들과 learning algorithm에서, double descent는 EMC의 함수로써 나타난다고 가정한다.

EMC의 정의는 다음과 같다. 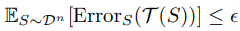zero training error(error가 epsilon보다 작은 경우)를 만족하는 조건 하에서, 최대가 되는 n 이 EMC의 정의다.

T는 training procedure, epsilon은 threshold, S는 (input, label)의 set. 총 n개의 data가 있음.

T(S)는 input을 output으로 mapping 시키기 위한 training procedure를 의미함.

그래서 결국 EMC는 T(w.r.t distribution D)에 대한 값이다. training procdure에 대한. 그래서 모델의 복잡도가, n보다 작으면, data 개수 n보다, 복잡도가 작으면, 학습하면 잘 학습된다.

under-parameterised regime: 모델의 복잡도(EMC)가 n보다 훨씬 작으면, T의 복잡도를 증가시키면, test error를 감소시킬 것이다. over-parameterised regime: 모델의 복잡도(EMC)가 n보다 훨씬 크면, T의 복잡도를 증가시키면, test error를 증가시킬 것이다. critically parameterised regime: 모델의 복잡도(EMC)가 n과 비슷하면, T의 복잡도를 증가시키면, test error를 증가시키거나 감소시킬 것이다.

결국 double descent curve를 보았을 때, x축을 resnet의 width(channel)수, 즉 parameter 수라고 했을 때, 여기서도, epoch을 고정시키면, double descent curve가 나타나고,

x축을 model complexity를 고정시켜서, epoch으로만 해도, double descent curve가 나타난다.

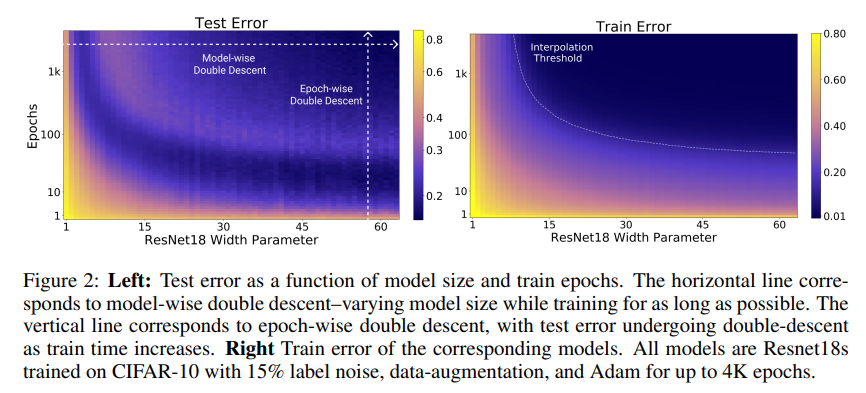
double descent curve

https://storage.googleapis.com/xavierbresson/lectures/CS3244/lecture06_overfitting_regularization.pdf

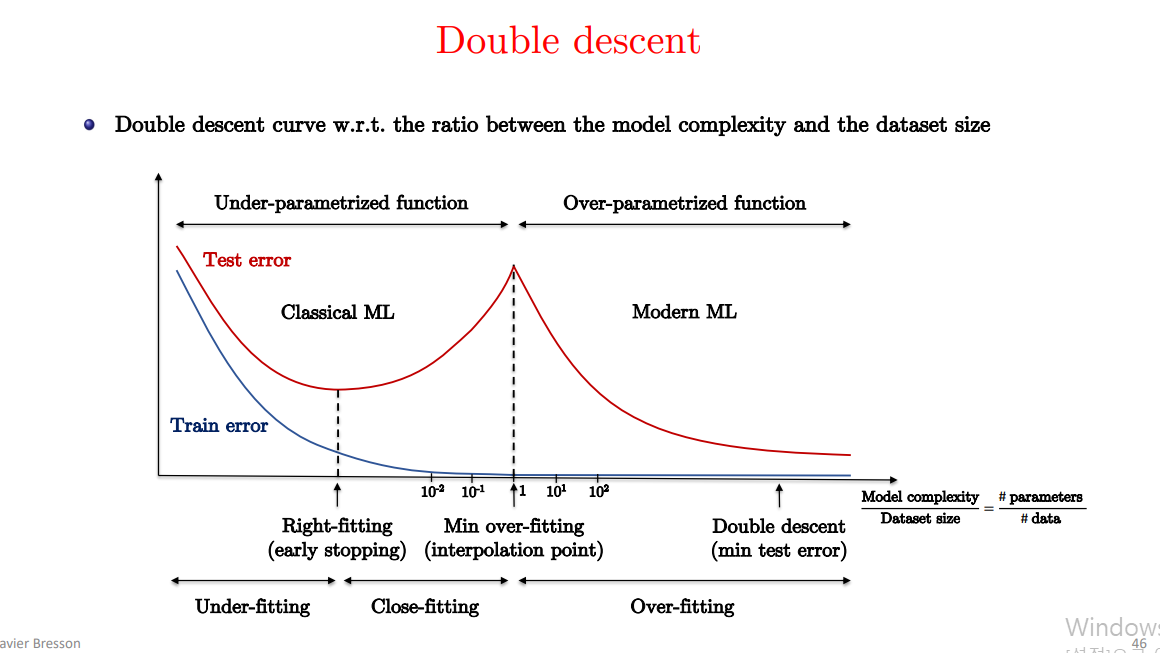
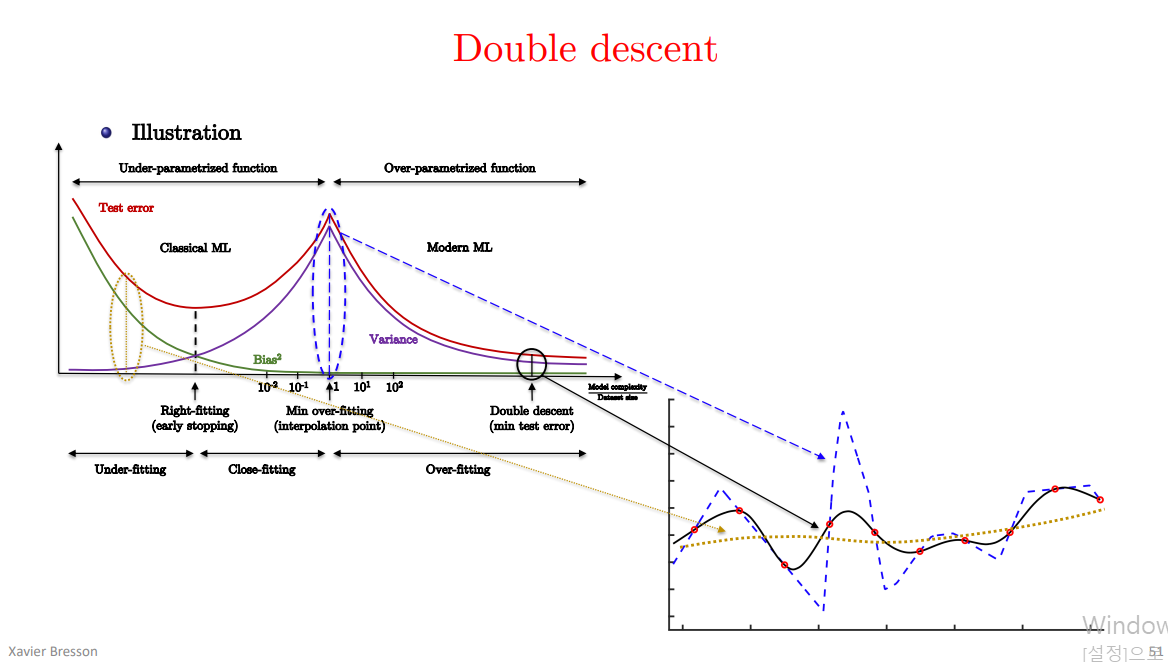
Interpolation의 의미:

• “Interpolation”이라는 용어는 모델이 훈련 데이터를 정확히 맞추는 상태를 가리킵니다. 즉, 모델이 모든 훈련 데이터 포인트를 정확하게 예측(interpolate)할 수 있을 때를 의미합니다.
• 이 상태에서는 모델의 복잡도가 데이터의 복잡도와 비슷해지면서, 훈련 데이터의 모든 포인트를 완벽하게 설명할 수 있습니다.