Blog Full Notice
back to main page
한달동안 배운것들: convolution filter 개수, MLE/MAP, gradient in matrixes
motivation: 한달동안 배운 것들을 정리해보자. convolution filter 개수, MLE/MAP, gradient in matrixes
1.
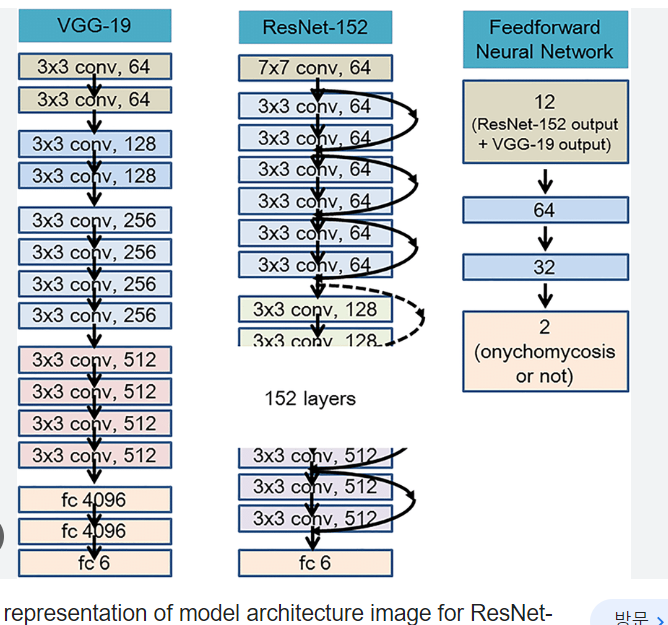
이런 architecture 이미지가 있다고 했을 때, 64, 128, 256 의 숫자는 c_out을 의미하는 것. 즉 convolution filter 개수가 64개인 것.
CNN에서, feature map에서, c_in이 32, c_out이 64면, 다음 feature map의 depth(개수)는 64다.
2.
posterior = likelihood * prior / evidence
에서, llikelihood와 probability의 개념의 차이는, 확률은 넓이고, likelihood는 그 함수의 값을 의미하는 것이다.
3.
3-1.
MLE, MAP. MLE는 likelihood를 최대화, MAP은 posterior prob를 최대화.
 출처: https://niceguy1575.medium.com/mle%EC%99%80-map%EC%9D%98-%EC%B0%A8%EC%9D%B4-7d2cc0bee9c
출처: https://niceguy1575.medium.com/mle%EC%99%80-map%EC%9D%98-%EC%B0%A8%EC%9D%B4-7d2cc0bee9c
근데 이렇게 곱셈으로 나타낼 수 있는 이유는, iid가 independent and identical distribution의 약자인데, 여기서 independent가 조건부독립임.
즉 (hyper)parameter(가우시안이면 parameterized distribution이니깐 mean과 variance가 될것.) space에서 정의에 의해서 조건부독립은 P(A,B|C) = P(A|C)P(B|C) 라서,
 이 수식이 성립하는 것.
이 수식이 성립하는 것.
왜 이렇게 쓸 수 있는 것이냐면, 결국 확률분포가 다 같은 분포라는 것(i.g. 다 가우시안 분포)라는 것을 가정하는 것.
</br>



3-2.
출처: https://hyeongminlee.github.io/post/bnn002_mle_map/
MLE에서
4.
gradient
gradient란 무엇인가?
다변수 함수(multivariate) f(x)가 있다고 해보자. x는 행벡터를 의미. 즉 x1, … , xn의 변수를 가지는 벡터다. 이 상황에서, f(x)를 모든 변수 x1,…,xn에 대해서 편미분하는 것을 gradient라고 한다. 예를 들어서, \(f(x,y,z) = x^2 + xy + zy\)라고 하자. 그러면 이것의 gradient는 \(\nabla_{\textbf{x}}f(x,y,z) = \begin{equation} \begin{bmatrix} 2x+y \\ x+z \\ y \\ \end{bmatrix} \end{equation}\) 가 된다.
gradient의 기호는, 벡터 x에 대해서 미분한다고 해서, \(\nabla_{\textbf{x}}\) 이렇게 표시한다.
즉 gradient는 \(\nabla_{\textbf{x}}f(\textbf{x}) = \begin{equation} \begin{bmatrix} \frac{\partial{f}}{\partial{x_1}} \\ \frac{\partial{f}}{\partial{x_2}} \\ \frac{\partial{f}}{\partial{x_3}} \\ \end{bmatrix} \end{equation}\)
이런 식으로 계산하게 되는 것이다.
jacobian
multivariate인 함수가 여러개 있다고 해보자. 즉 함수도 벡터가 된 것이다.
f(x) 이런 상황. 이런 예시로는,
\(\textbf{f}(\textbf{x}) = \begin{equation} \begin{bmatrix} f_1(x,y,z) \\ f_2(x,y,z) \\ f_3(x,y,z) \\ \end{bmatrix} \end{equation}\) \(= \begin{equation} \begin{bmatrix} x+y+z \\ xy+yz+xz \\ xyz \\ \end{bmatrix} \end{equation}\) 인 상황이다. 이런 상황에서 jacobian은 각 행에 대해서 gradient를 구하면 된다.
\[\nabla_{\textbf{x}}\textbf{f}(x,y,z) = \begin{equation} \begin{bmatrix} 1 &1&1 \\ y+z&x+z&x+y \\ yz&xz&xy \\ \end{bmatrix} \end{equation}\]</br>
즉 jacobian은 \(J(\textbf{f}(\textbf{x})) = \begin{equation} \begin{bmatrix} \nabla_{\textbf{x}}f_1(x,y,z)^T \\ \nabla_{\textbf{x}}f_2(x,y,z)^T \\ \nabla_{\textbf{x}}f_3(x,y,z)^T \\ \end{bmatrix} \end{equation} = \nabla_{\textbf{x}}\textbf{f}(x,y,z)\) 이렇게 표현할 수 있는 것이다.
\[J(\textbf{f}(\textbf{x})) = \begin{equation} \begin{bmatrix} \nabla_{\textbf{x}}f_1(x,y,z)^T \\ \nabla_{\textbf{x}}f_2(x,y,z)^T \\ \nabla_{\textbf{x}}f_3(x,y,z)^T \\ \end{bmatrix} \end{equation} = \nabla_{\textbf{x}}\textbf{f}(x,y,z)\] \[\nabla_{\textbf{x}}f(\textbf{x}) = \begin{equation} \begin{bmatrix} \frac{\partial{f_1}}{\partial{x_1}} & \frac{\partial{f_1}}{\partial{x_2}} & \frac{\partial{f_1}}{\partial{x_3}} \\ \frac{\partial{f_2}}{\partial{x_1}} & \frac{\partial{f_2}}{\partial{x_2}} & \frac{\partial{f_2}}{\partial{x_3}} \\ \frac{\partial{f_3}}{\partial{x_1}} & \frac{\partial{f_3}}{\partial{x_2}} & \frac{\partial{f_3}}{\partial{x_3}} \\ \end{bmatrix} \end{equation}\]Hessian
헤시안은
multivariate function f(x)를 gradient로 하나의 열벡터를 만들고, 그 열벡터는 어떻게 보면 multivariate function들이 여러개 있는 f(x)가 된다. 그거를 이제 jacobian을 하면,
 이렇게 된다.
이렇게 된다.
5.
그렇다면 gradient를 어떻게 구할까?
5.1
 이런 상황에서는, \(b^Tx\)는 그냥 multivariate function이다. 이거를 gradient를 구하면, b가 나온다.(행벡터)
이런 상황에서는, \(b^Tx\)는 그냥 multivariate function이다. 이거를 gradient를 구하면, b가 나온다.(행벡터)
</br> </br>
5.2
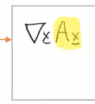 이거는 어떻게 될까?
이거는 어떻게 될까?
A를  이렇게 보면,
이렇게 보면,
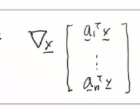 이렇게 되고, 이거는 vector of multivariate function이어서, jacobian이 된다. 즉 이 상황에서 각 row에 대해서 gradient를 구하게 되면, A가 나오게 된다.
이렇게 되고, 이거는 vector of multivariate function이어서, jacobian이 된다. 즉 이 상황에서 각 row에 대해서 gradient를 구하게 되면, A가 나오게 된다.
출처: https://atmos.washington.edu/~dennis/MatrixCalculus.pdf








5.3

이런 form의 gradient는 어떻게 될까?
위에 답이 나와있다.
L2, L1 regularization
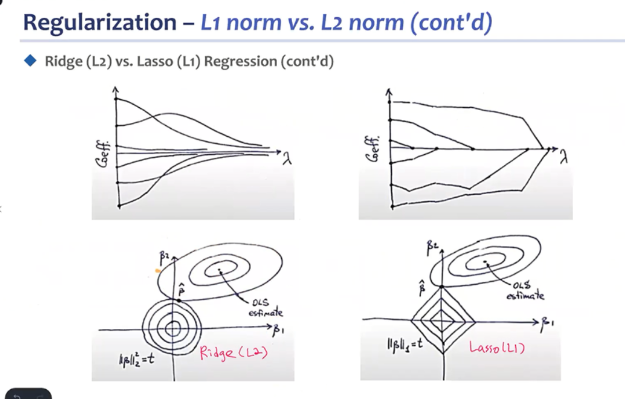
constraint optimization problem으로 바꿀 수 있다.
l1 norm은 sparsity, l2 norm은 weight regularization에 쓰인다. 결국 l1은 위 그림처럼 특정 매개변수가 0에 수렴하게 될 수 있음.
댓글남기기